This utility lets you draw custom and colorful Pythagoras fractals. We offer you more than twenty options to create a truly personalized fractal. The options are divided into three categories. The first category is for adjusting the image size and canvas dimensions, iterations, tree angle, and the proportions of the base rectangle from which the whole tree evolves. The second category is for adjusting colors and gradient. You can paint the fractal with a five-color palette. The first two colors define the background gradient, the next two are responsible for the tree gradient, and the last one sets the line drawing color. The third category lets you quickly switch between predefined Pythagoras tree species. The species include coniferous, semi-coniferous, cypress, and randomized trees. Fun fact – there are infinitely many logarithmic spirals hidden in a Pythagoras tree and they can be found by starting with any square and always following the closest square that goes to the left or right. Created by fractal fans from team Browserling. Fractabulous!
This utility lets you draw custom and colorful Pythagoras fractals. We offer you more than twenty options to create a truly personalized fractal. The options are divided into three categories. The first category is for adjusting the image size and canvas dimensions, iterations, tree angle, and the proportions of the base rectangle from which the whole tree evolves. The second category is for adjusting colors and gradient. You can paint the fractal with a five-color palette. The first two colors define the background gradient, the next two are responsible for the tree gradient, and the last one sets the line drawing color. The third category lets you quickly switch between predefined Pythagoras tree species. The species include coniferous, semi-coniferous, cypress, and randomized trees. Fun fact – there are infinitely many logarithmic spirals hidden in a Pythagoras tree and they can be found by starting with any square and always following the closest square that goes to the left or right. Created by fractal fans from team Browserling. Fractabulous!

This online browser-based tool illustrates Pythagoras fractal trees. The Pythagoras tree is one of the most popular fractals in the fractal tree family that includes v-fractal and fractal canopy. The classic version of this fractal begins with a square but we've also added a modified version that begins with a rectangle. To construct the next iteration, take the square and build a right triangle on top of it so that the top edge of the square is the hypotenuse. Then, construct squares (or rectangles) on both sides of the triangle. This is the second level of the fractal. This construction is repeated recursively on each of the two new squares, and then recursively again on the new squares, until infinity. The limit of this construction is called the Pythagoras fractal (or the Pythagorean tree). If the sides of the interlevel triangle are equal, then the Pythagorean fractal will be symmetric. If the left corner is smaller than the right, the tree will tilt to the left side but if the right angle is less than the left, the tree will tilt to the right side. When the symmetric tree is drawn with a unit square as the base figure, the entire fractal (at infinite iteration) will fit exactly inside a 6x4 rectangle. Mind blowing and ingenious at the same time, or as we love to say – fractabulous!
This online browser-based tool illustrates Pythagoras fractal trees. The Pythagoras tree is one of the most popular fractals in the fractal tree family that includes v-fractal and fractal canopy. The classic version of this fractal begins with a square but we've also added a modified version that begins with a rectangle. To construct the next iteration, take the square and build a right triangle on top of it so that the top edge of the square is the hypotenuse. Then, construct squares (or rectangles) on both sides of the triangle. This is the second level of the fractal. This construction is repeated recursively on each of the two new squares, and then recursively again on the new squares, until infinity. The limit of this construction is called the Pythagoras fractal (or the Pythagorean tree). If the sides of the interlevel triangle are equal, then the Pythagorean fractal will be symmetric. If the left corner is smaller than the right, the tree will tilt to the left side but if the right angle is less than the left, the tree will tilt to the right side. When the symmetric tree is drawn with a unit square as the base figure, the entire fractal (at infinite iteration) will fit exactly inside a 6x4 rectangle. Mind blowing and ingenious at the same time, or as we love to say – fractabulous!
In this example, we set the left bending angle equal to 45 degrees, and the right angle is calculated automatically as follows: 90 - 45 = 45 degrees. With these angles, the interlevel triangles are isosceles, and as a result, the whole tree has mirror symmetry with respect to the vertical axis going through the middle of the trunk. We generate 10 levels of branches, using all five colors in the palette. We set a mountain-meadow-green to deep-sea-green color gradient for the background, a white to pink-flamingo color gradient for the tree, which is applied from the tree root to twigs, and a pompadour color line for the square border.
In this example, the left and right angles alternate at each recursive level. As a result, the Pythagoras fractal has a shape of a coniferous tree. We set the first left bending angle to 35 degrees that makes our tree to be tilted to the left side. We also set the proportions of the base rectangle to 1:2 to make the tree thinner and higher. To make the tree fit nicely in the canvas, we slightly lengthen the height of the canvas to 900 pixels, with a width of 800 pixels, and draw 12 recursive levels of rectangles.
In this example, we generate a semi-coniferous Pythagoras tree. That means that the left and right angles alternate every two levels. That is, on the first and second level, the left bend angle is 56°, on the third and fourth 90° - 56° = 34°, on the fifth and sixth 56° again, and so on. We set the width of the base rectangle to 20% less than its height and perform 13 iterative steps. We use an individual branch gradient from gorse-yellow to flamenco-orange color for the tree fill and curious-blue to Stratos-blue color gradient for the background.
In this example, the Pythagoras fractal grows to an extraordinary shape because the height of the base rectangle is set to be 3 times smaller than its width. With these base figure dimensions and the cypress tree type, it looks more like a bush than a tree. We iterate this bush for 11 stages and set the bending angle is 38 degrees. We also use a rectangular canvas of 800 by 600 pixels and padding of 10 pixels around the trunk and bush tips.
In this example, the tool randomly selects the rotation angle for each iterative level and keeps it constant for all triangles on that level. However, as we have also activated the tree symmetrization option, the closer we get to the last iteration, the closer the angle gets to 45 degrees. At the last level, all the angles are 45 degrees. We set the rectangle ratio to 2:5 and generate 12 recursive stages. For the color palette, we use a deep-blue to congress-blue color gradient for the background and aqua to magenta color gradient for the branches.
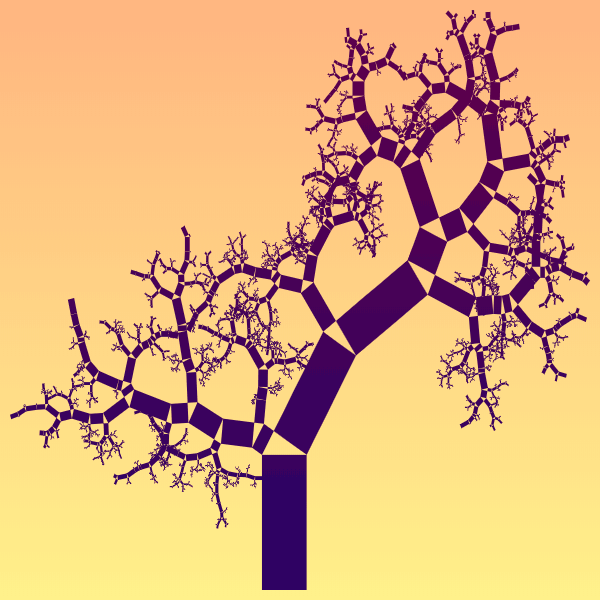
This example randomizes both key tree properties. The bending angle for each branch is chosen arbitrarily and the proportions of each rectangle are also selected randomly. Thus, we get an absolutely randomized Pythagorean tree with branches and twigs going in all possible directions. We color this tree with a paua to pompadour color gradient in the tree direction and calculate 15 iterations.
You can pass options to this tool using their codes as query arguments and it will automatically compute output. To get the code of an option, just hover over its icon. Here's how to type it in your browser's address bar. Click to try!
Walk the Hilbert fractal and enumerate its coordinates.
Walk the Peano fractal and enumerate its coordinates.
Walk the Moore fractal and enumerate its coordinates.
Encode the Hilbert fractal as a string.
Encode the Peano fractal as a string.
Encode the Moore fractal as a string.
Encode the Cantor set as a string.
Encode the Heighway Dragon as a string.
Encode the Sierpinski fractal as a string.
Generate a Sierpinski tetrahedron (tetrix) fractal.
Generate a Cantor's cube fractal.
Generate a Sierpinski-Menger fractal.
Generate a Jerusalem cube fractal.
Generate a Jeaninne Mosely fractal.
Generate a Mandelbrot tree fractal.
Generate a Barnsley's tree fractal.
Generate a Barnsley's fern fractal.
Generate a binary tree fractal.
Generate a ternary tree fractal.
Generate a dragon tree fractal.
Generate a de Rham curve.
Generate a Takagi-Landsberg fractal curve.
Generate a Peano pentagon fractal curve.
Generate a tridendrite fractal curve.
Generate a Pentigree fractal curve.
Generate a lucky seven fractal curve.
Generate an Eisenstein fractions fractal curve.
Generate a Bagula double five fractal curve.
Generate a Julia fractal set.
Generate a Mandelbrot fractal set.
Generate a Mandelbulb fractal.
Generate a Mandelbox fractal.
Generate a Buddhabrot fractal.
Generate a Burning Ship fractal.
Generate a toothpick sequence fractal.
Generate an Ulam-Warburton fractal curve.
Generate an ASCII fractal.
Generate an ANSI fractal.
Generate a Unicode fractal.
Generate an emoji fractal.
Generate a braille code fractal.
Generate a fractal in audio form.
Create a fractal that looks like one but isn't a fractal.
Generate a fractal from any text.
Generate a fractal from a string.
Generate a fractal from a number.
Join any two fractals together.
Create a completely random fractal.
Set up an arbitrary IFS system and iterate it.
Recursively transform an image using IFS rules.
Run infinite compositions of analytic functions.
Create a surface that mimics a natural terrain.
Create a fractal surface via Brownian motion.
Apply fractal algorithms on your image and make it self-similar.
Find fractal patterns in any given image.
Find fractal patterns in any given text.
Find fractal patterns in any given number.
Tessellate a plane with fractals.
Run a cellular automaton with custom rules.
Play Conway's Game of Life on an infinite grid.
Subscribe to our updates. We'll let you know when we release new tools, features, and organize online workshops.
Enter your email here
We're Browserling — a friendly and fun cross-browser testing company powered by alien technology. At Browserling our mission is to make people's lives easier, so we created this collection of fractal tools. Our tools have the simplest user interface that doesn't require advanced computer skills and they are used by millions of people every month. Our fractal tools are actually powered by our web developer tools that we created over the last couple of years. Check them out!