This browser-based tool multiplies all digits in an integer and prints their product in the output. You can choose between two multiplication modes – single-pass mode that simply multiplies all digits together or multi-pass mode that multiplies all digits together recursively until a single-digit root value is left. You can also skip zeros during the multiplication process to avoid the zero product. Created by math nerds from team Browserling.
This browser-based tool multiplies all digits in an integer and prints their product in the output. You can choose between two multiplication modes – single-pass mode that simply multiplies all digits together or multi-pass mode that multiplies all digits together recursively until a single-digit root value is left. You can also skip zeros during the multiplication process to avoid the zero product. Created by math nerds from team Browserling.
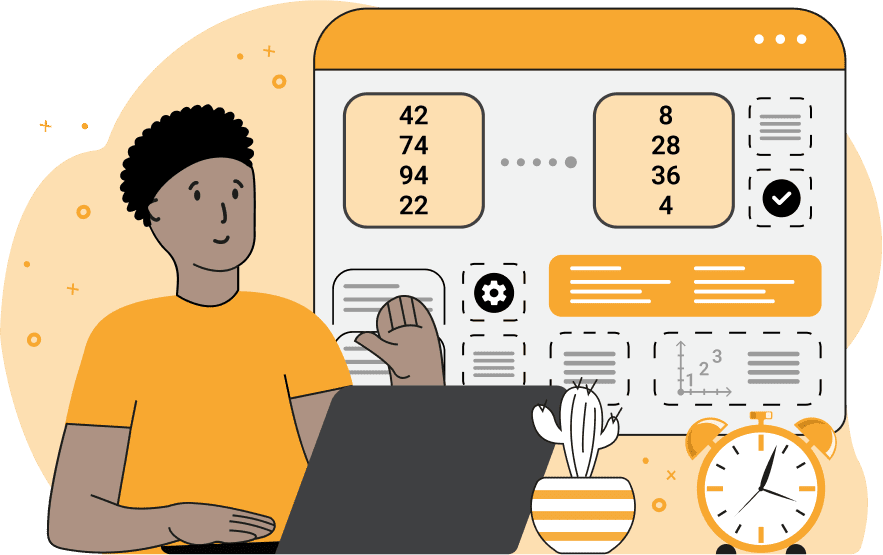
With this online utility, you can multiply all the digits of an integer and find their product. For example, if the input contains the integer 1237, then after multiplying its digits 1×2×3×8, the output 48 will be produced. The input may contain arbitrary large integers with any number of digits. If the "Repeated Digital Product" option is disabled (by default it's disabled), the program prints this one value and stops. If the "Repeated Digital Product" option is enabled, then the program restarts the algorithm and recursively applies it to the previous product. For example, 1×2×3×8 = 48, then 4×8 = 32, then 3×2 = 6. When a one-digit value is reached, the algorithm stops and displays all intermediate results on the screen. The single-digit integer resulting from repeated multiplications is called the repeated digital root. If there's at least one occurrence of a zero in integer's digits, the entire product becomes zero. If you use the "Skip Zeros" option, then it skips all zero factors and the result is non-zero. Integerabulous!
With this online utility, you can multiply all the digits of an integer and find their product. For example, if the input contains the integer 1237, then after multiplying its digits 1×2×3×8, the output 48 will be produced. The input may contain arbitrary large integers with any number of digits. If the "Repeated Digital Product" option is disabled (by default it's disabled), the program prints this one value and stops. If the "Repeated Digital Product" option is enabled, then the program restarts the algorithm and recursively applies it to the previous product. For example, 1×2×3×8 = 48, then 4×8 = 32, then 3×2 = 6. When a one-digit value is reached, the algorithm stops and displays all intermediate results on the screen. The single-digit integer resulting from repeated multiplications is called the repeated digital root. If there's at least one occurrence of a zero in integer's digits, the entire product becomes zero. If you use the "Skip Zeros" option, then it skips all zero factors and the result is non-zero. Integerabulous!
In this example, we calculate the digit product of several integers in parallel. Each input integer is on its own line and each result is also on its own line. If there's at least one zero in the integer, then the entire product is turned to zero (see the integer on line four). The signs of integers are preserved in the results (see integers on lines two and three).
In this example, we have enabled the "Repeated Digital Product" option that iteratively calculates the multiplicative digit root for seven different integer values. The program automatically determines how many times to apply the multiplication function on the results to get a one-digit value as the final product.
This example contains integers that each have one or more zero-digits. For such integers, the product of digits is always zero. To get a non-zero result, we use the skip zero digits option. It drops zeros from the input and the multiplication algorithm safely produces a non-zero result.
You can pass input to this tool via ?input query argument and it will automatically compute output. Here's how to type it in your browser's address bar. Click to try!
Create a drawing that visualizes von Neumann hierarchy of sets.
Create a sudoku puzzle.
Create a list of neat-looking integers (called magic integers).
Generate a list of tuples of integers with n elements.
Quickly convert integers to base one.
Quickly convert base one to integers.
Quickly convert integers to base two.
Quickly convert base two to integers.
Quickly convert integers to base eight.
Quickly convert base eight to integers.
Quickly convert integers to base sixteen.
Quickly convert base sixteen to integers.
Quickly encode integers to base-64.
Quickly decode base-64 to integers.
Quickly convert integers to a custom base.
Quickly encode integers to HTML encoding.
Quickly decode HTML entities to integers.
Quickly encode integers to URL (percent) encoding.
Quickly decode URL-encoded integers.
Quickly convert a signed integer to an unsigned integer.
Quickly convert an unsigned integer to a signed integer.
Generate a list of random integers.
Check if the given integers are palindromes.
Create a matrix whose entries are all integers.
Create a vector with integer coefficients.
Quickly calculate the average value of integers.
Quickly calculate the average value of integer digits.
Quickly randomly select a digit from an integer.
Find which of the given integers is the biggest or smallest.
Limit integer values to a range.
Limit integer digit values to a range.
Create multiple copies of the input integers.
Create multiple copies of digits of input integers.
Rotate the digits of an integer to the left or right.
Move the digits of an integer to the left or right.
Quickly find the difference of a bunch of integers.
Quickly apply the bitwise AND operation to integers.
Quickly apply the bitwise OR operation to integers.
Quickly apply the bitwise XOR operation to integers.
Quickly apply the bitwise NOT operation to integers.
Quickly apply the bitwise NAND operation to integers.
Quickly apply the bitwise NOR operation to integers.
Quickly apply the bitwise NXOR operation to integers.
Quickly divide two or more integers.
Quickly divide the digits of an integer.
Add -st, -nd, -rd, -th suffixes to integers to make them ordinals.
Remove -st, -nd, -rd, -th suffixes from ordinals to make them ints.
Find integers that match a filter (greater, less, equal).
Add padding to integers on the left side.
Add padding to integers on the right side.
Position all integers so that they align on the right.
Position all integers so that they align in the middle.
Turn all integers into positive integers.
Turn all integers into negative integers.
Rewrite an integer in fractional form.
Extract the numerator and denominator from a fraction.
Search for all occurrences of an integer and replace it.
Create a regex that matches the given integers.
Create integers that match the given regular expression.
Create relatively tiny integers.
Create relatively huge integers.
Create a sequence of oscillating integers, such as 123212321.
Create multiple integer sequences at once.
Slightly change an integer so it has an error.
Slightly change integer digits so there are errors.
Apply fuzzing to integers and add perturbations.
Apply fuzzing to integer digits and add digit perturbations.
Add highlighting to certain integers.
Add highlighting to certain integer digits.
Add color to integers based on a condition.
Add color to individual digits in the given integers.
Quickly assign colors to integers and draw them as pixels.
Quickly assign integer values to pixel colors and print them.
Make the digits of an integer go in a spiral shape.
Make the digits of an integer go in a circle.
Make the digits of an integer go in a diamond shape.
Fill a box with certain width and height with digits.
Use ASCII art to convert integers to 2-dimensional drawings.
Use ASCII art to convert integers to 3-dimensional drawings.
Decompose an integer into ones, tens, hundreds, etc.
Generate an ordered list of increasing integers.
Generate an ordered list of decreasing integers.
Quickly find various information about the given integers.
Find hidden patterns of numbers in integers.
Find the Shannon entropy of an integer.
Subscribe to our updates. We'll let you know when we release new tools, features, and organize online workshops.
Enter your email here
We're Browserling — a friendly and fun cross-browser testing company powered by alien technology. At Browserling our mission is to make people's lives easier, so we created this collection of integer tools. Our tools have the simplest user interface that doesn't require advanced computer skills and they are used by millions of people every month. Our integer tools are actually powered by our programming tools that we created over the last couple of years. Check them out!

